O Som: Propagando as características de uma Onda
Em um dia calmo, próximos, de uma árvore, podemos ouvir o som das folhas balançando ao vento. Trata-se de dois fenômenos que não aconteceriam sem a presença do ar: o balançar das folhas e o som.
Quando há diferença de pressão entre duas regiões da atmosfera, ocorre um deslocamento de ar da região de maior pressão para a de menor pressão: o vento. Se essa diferença for pequena, soprará uma leve brisa, mas, se for muito grande, fortes ventanias varrerão a região.
Veja o slide logo abaixo e depois siga para o resumo.
O som
Os sons também são gerados por diferenças de pressão variáveis no tempo, mas tais diferenças devem ser próximas no espaço e no tempo. Por isso, um som sempre é causado por algo que vibra. Pode ser uma corda, como em um violão, uma membrana, como em um tamborim, uma coluna de ar, como em uma flauta, ou lâminas de aço, como em uma gaita.
Para compreendermos como um som é produzido, imaginemos uma lâmina com uma extremidade presa, e a outra vibrando. Enquanto vibra em cada direção em que se move, a lâmina pressiona a camada de ar que está à sua frente, ao mesmo tempo que a pressão de ar diminui na parte de trás. Portanto, de um lado da lâmina há compressão de ar, com aumento da pressão, e, do outro, há descompressão de ar, com a redução da pressão.
Quando a lâmina inverte o sentido do movimento, ocorre uma inversão também nas regiões do ar que são comprimidas e descomprimidas. Essas compressões e descompressões se propagam para as camadas de ar imediatamente próximas, e destas para as seguintes, gerando uma sequência de perturbações que se espalham pelo espaço, a que chamamos de onda mecânica.
Onda mecânica é a alteração de alguma propriedade de um meio, como, por exemplo, pressão do ar ou tensão em um sólido, que, a partir do ponto em que ocorreu, se transmite de forma homogênea e sucessiva para os pontos vizinhos.
Há muitos tipos de ondas mecânicas além das sonoras, por exemplo, as ondas do mar, as da superfície da água em uma piscina ou as de uma corda.
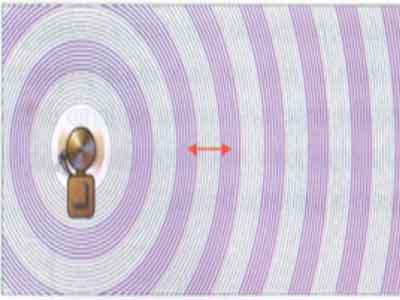 Cada uma delas possui características próprias, mas todas têm algo em comum: transportam energia de movimento de um ponto a outro, algumas a grandes distâncias, porém, não levam junto a matéria, que apenas oscila no meio por onde elas se propagam. As partículas desse meio oscilam em torno de um ponto de equilíbrio e transmitem essa energia de movimento às partículas vizinhas.
Cada uma delas possui características próprias, mas todas têm algo em comum: transportam energia de movimento de um ponto a outro, algumas a grandes distâncias, porém, não levam junto a matéria, que apenas oscila no meio por onde elas se propagam. As partículas desse meio oscilam em torno de um ponto de equilíbrio e transmitem essa energia de movimento às partículas vizinhas.
As ondas podem ser transversais, quando a direção de vibração das partículas do meio é perpendicular à direção de propagação da onda, ou longitudinais, quando as partículas do meio vibram na mesma direção de propagação da onda.
Ondas que apresentam características constantes, porque se repetem constantemente, são chamadas de ondas periódicas, por exemplo, as ondas causadas por uma torneira pingando em um tanque cheio de água. As gotas caindo regularmente sobre a superfície da água, provocam distúrbios no líquido, que se propagam na forma de ondas circulares, as quais se afastam do ponto de impacto, fazendo as moléculas que compõem o meio oscilarem regularmente. Podemos colocar um pequeno pedaço de isopor e, ao observar o que acontece com ele, identificaremos que ele sobe e desce conforme cada onda passa.
Uma fotografia da superfície do tanque revela a característica periódica da onda no espaço: nela identifica-se a repetição de um mesmo padrão de forma enquanto a onda se afasta de sua origem. Por sua vez, a periodicidade no tempo pode ser identificada observando o padrão que se repete em cada ponto do meio em que a onda se propaga; verificamos esse padrão observando o movimento do isopor: vemos a repetição de uma oscilação para cima e para baixo em uma mesma posição.
Características de uma onda periódica
Recorda-se da época em que ainda brincava com corda? Já faz um bom tempo que a “onda” era pular corda, e é essa mesma corda que nos ajudará a entender as características físicas de uma onda periódica.
Se prendermos a extremidade de uma corda e movimentarmos a outra extremidade para cima e para baixo, com movimentos iguais e repetitivos, criaremos uma onda periódica que se propaga ao longo da corda.
Se a perturbação do meio é isolada, sem repetição contínua, cria-se um abalo, denominado pulso.
Muitas ondas não são periódicas, e muitos pulsos ocorrem e propagam-se nos meios sem se repetirem; por exemplo, uma explosão gera perturbação no ar, causando um grande e instantâneo aumento de pressão, que se desloca rápida e violentamente para as regiões de pressão mais baixa, criando um pulso mecânico, chamado onda de choque, que pode ser devastador. Quando um ponto é atingido pela onda de choque, ocorre um súbito aumento de pressão local, que decai após a passagem do pulso.
Os pontos da corda de deslocamento máximo no sentido positivo do eixo y denominam-se cristas da onda; os vales, ou depressões, são pontos de deslocamento máximo no sentido negativo do eixo y. Observe: foi produzida uma sequência de ondas periódicas denominada trem de ondas, que se propaga com velocidade v constante.
Para criar a variedade de sons que estamos habituados a ouvir nas rádios, nos CDs, e em tantas outras mídias, utilizamos o alto-falante. Este instrumento faz vibrar o ar para emitir o som por meio de um cone que é movimentado por um eletroímã de acordo com o som que deve ser produzido. O alto-falante cria regiões de compressão e rarefação do ar à sua frente, as quais se propagam na forma de uma onda, fazendo com que a pressão do ar sofra diminutas variações tanto no espaço quanto no tempo, produzindo o som que ouvimos.
Esquematicamente, temos:
- Comprimento de onda(X): Em um trem de ondas, definimos comprimento de onda (X) como a distância entre dois pontos consecutivos da onda que vibram em concordância de fase. Para que dois pontos estejam em concordância de fase é necessário que assumam o mesmo deslocamento vertical e executem, rigorosamente, o mesmo movimento. Observe a figura a seguir. Os pontos D, J e P, por exemplo, estão em concordância de fase.
Os pontos E e I apresentam o mesmo deslocamento vertical, mas não estão em concordância de fase; enquanto E sobe, I desce. Os pontos D e G vibram em oposição de fase. Assim, o comprimento de onda X pode ser expresso pelas distâncias entre os pontos D-J, J-P, E-K, F-L, N-T, G-M e M-S indicados na figura a seguir:
- Amplitude (A):Definimos como amplitude de uma onda a distância que separa a posição de equilíbrio das posições extremas da onda.
- Período de uma onda (T):Definimos como período de uma onda o intervalo de tempo utilizado para realizar uma oscilação completa. Em outras palavras, é o intervalo de tempo decorrido para que a onda se propague pela distância de um comprimento de onda. Observe a sequência a seguir:
Para uma situação em que seja produzido um número de ondas completas igual a n em um inter valo de tempo At, temos: T = At/n
Frequência de uma onda (f): Definimos frequência de oscilação de uma onda o número de comprimentos de onda que se propaga por unidade de tempo, ou seja, a quantidade de oscilações realizadas por unidade de tempo.




